Cadcom/manuel d'utilisation
 
RETROPROPAGATION
Ce réseau comprend:

   une seule couche d'entrée.
   une seule couche de sortie /par variable à corréler
   une ou plusieurs couches cachées.
 
  
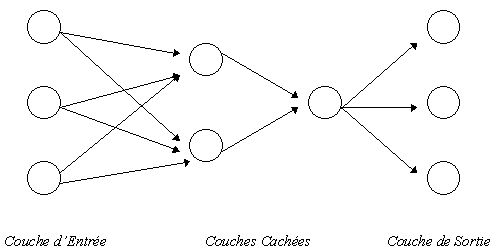         Un neurone i de la couche intermédiaire k + 1 reçoit en entrée 
         une somme pondérée fonction de l'état des neurones précédents.
            Sa position au temps t(itération) est connue en:
           calculant la somme pondérée à l'entrée (somme pour tous les neurones
             de la couche k de l'activation du neurone j de la couche k multiplié
             par le poids de la connexion du neurone j à i). 
           en bridant cette valeur à l'aide de la fonction de transfert.
             (0 ou 1,actif ou inhibé)0
           en envoyant sa valeur de sortie aux neurones de la couche suivante
1) Les Parametres
    Le nombre de neurones en entrée et sortie est déterminé
    par la taille du fichier à analyser.
    .Les neurones d'entree correspondent aux descripteurs(ou
     colonnes),les neurones de sortie correspondent aux variables à
     corréler(dernier descripteur ou dernière colonne)
    Le nombre de couches intermediaires(ou couches cachees)
    varie en fonction de la complexite du probleme(en general
    une ou 2 couches suffisent).
    Le nombre de neurones dans les couches cachees est
    egalement variable
 
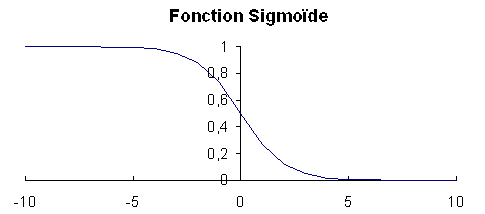
 2)La fonction d'activation
   La fonction d'évaluation couramment utilisée est la fonction
   sigmoide:
 
f(x)=sigma/(1+exp(-t(x-sigma/2)))
 
     ou:
      sigma represente l'intervalle du signal de sortie:il
        est pris à 1.0.
        (les données en entrée sont automatiqement prétraitées
         pour se trouver entre 0 et 1,en fait 0.05 et 0.95)
      t (temperature) représente la non linearite du système:
         (t proche de 0,la fonction est lineaire)
  
3)L'apprentissage
l’apprentissage consiste en un entraînement du réseau. 
On présente au réseau des entrées et on lui demande de modifier sa pondération
de telle sorte que l’on retrouve la sortie correspondante.
L’algorithme consiste dans un premier temps à propager vers l’avant 
les entrées jusqu'à obtenir une entrée calculée par le réseau. 
La seconde étape compare la sortie calculée à la sortie réelle connue. 
On modifie alors les poids de telle sorte qu’à la prochaine itération,
l’erreur commise entre la sortie calculée et connue soit minimisée. 
Malgré tout, il ne faut pas oublier que l’on a des couches cachées. 
On rétro-propage alors l’erreur commise vers l’arrière jusqu'à la couche d’entrée
tout en modifiant la pondération.
On répète ce processus sur tous les exemples jusqu'à temps
que l’on obtienne une erreur de sortie considérée comme négligeable. 


4)L'algorithme de rétropropagation
    Considerons un réseau à 3 couches(entrée,cachée,sortie)
    Le fichier à analyser est scindé en deux parties:
       L'échantillon(en general 80% de la population à étudier)
       Le test(les 20% restants)
 
    4.1)La phase d'apprentissage("training")
       La phase de training consiste à déterminer les poids des
       connections entre neurones(W1ij et W2ij)sur l'échantillon.
       L'apprentissage est dit supervisé car on impose une entrée
       et une sortie.
       Les poids minimaux seront alors appliques sur le test
       pour verifier la justesse et la precision des calculs.
       
         Les poids initiaux sont initialisés aléatoirement.
         puis sont determinés par minimisation de la
         fonction coût du systeme,définie comme;
          Cout=erreur absolue(ypredit-yinitial)
         Deux recuits simulés sont appliqués ici:
         .Le premier pour déterminer la meilleure valeur de T
          dans la fonction sigmoide(le programme part de t=9 et
          décroit jusqua 0 )
         .Le second pour determiner la meilleure valeur du
          momentum  dans la boucle de minimisation du coût.
       Le systeme s'arrête soit parce qu il a trouvé un coût
       inferieur à la  valeur specifiée par l'utilisateur,soit
       parcequ'il a balayé tout l espace de température de la
       fonction sigmoide .
       
    4.2)La phase de validation
        Elle a pour but de tester le modéle sur le le % de population
        non utilisé en calculant:
          - les predictions correctes
          - les predictions incorrectes
          - les mauvaises predictions
        
 
 

(SOMMAIRE)

Webmaster:
Last revised:05/2000