La visualisation euclidienne d'un espace de Minkowski se fait en contractant cet espace à un espace de dimension inférieure d'une unité. Les modéles les plus courants de contraction sont les modéles de Klein ou de Poincaré(2D ou 3D)
Le modéle de KLEIN BELTRAMI
Le modéle de Klein-Beltrami d'une géometrie hyperbolique est défini comme l'ensemble de tous les points dans le disque ouvert D de rayon unité. Les "lignes" de cette geometrie sont des cordes ouvertes,cad des segments de ligne euclidiens avec des points terminaux sur la frontiére du disque
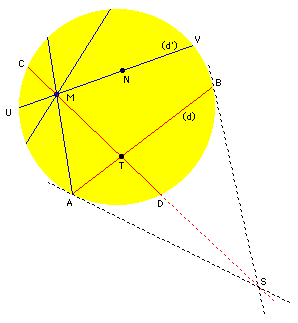
Soient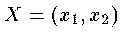
et 
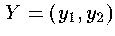2 points dans le disque de Klein-Beltrami .
Le produit de Minkowski est donné par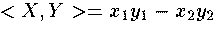 
.
La métrique du modéle de Klein-Beltrami est alors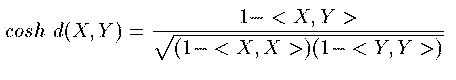
.
.
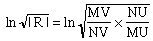Le modéle de POINCARE
Le modéle de Poincaré est défini par l'ensemble de tous les points dans le disque ouvert.D. Les"lignes" de l'espace hyperbolique sont representées par des arcs euclidiens qui intersectent perpendiculairement la frontiére du cercle D .
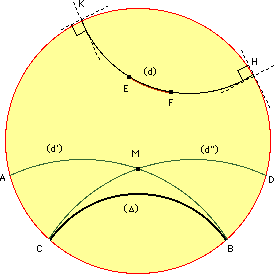
La métrique dans le disque de Poincare est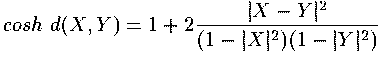 
.
Cette métrique est derivée de l'équation différentielle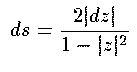 
Les isoméries entre modéles
De Klein à Minkowski
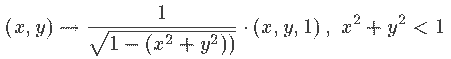
De Minkowski à Klein
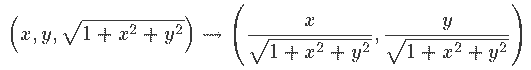
De Klein à Poincaré
En coordonnées polaires:
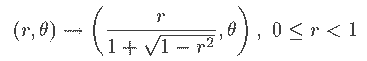
En coordonnées cartesiennes:
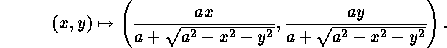
De Poincaré à Klein
En coordonnées polaires:
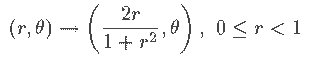
De Poincare à Minkowski
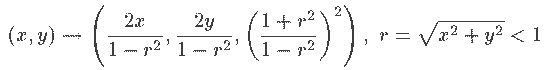
De Minkowski à Poincare
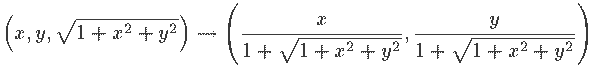
Webmaster:
Last revised:06/2001