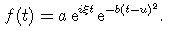CADCOM/MANUEL D'UTILISATION
LES TRANSFORMEES DE FOURIER
1)Introduction
L'analyse de Fourier est une analyse spectrale.Elle
repose sur la notion de fréquence,temps, périodicité.
 Une fréquence est l'inverse d'une
période.
Une fréquence est l'inverse d'une
période.
 Un signal monodimensionnel est
périodique de période T>0 s'il reste inchangé par une translation de T.
Un signal monodimensionnel est
périodique de période T>0 s'il reste inchangé par une translation de T.
 On appelle signal stationnaire un
signal dont le contenu fréquentiel ne change pas dans le temps.
On appelle signal stationnaire un
signal dont le contenu fréquentiel ne change pas dans le temps.
 Signal stationnaire
Signal stationnaire
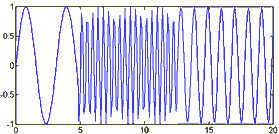 Signal non stationnaire
Signal non stationnaire
2)Définitions
Toute fonction périodique du temps x(t)
peut être décomposée en une somme infinie de sinus et cosinus dont les
fréquences commencent à zéro et augmentent par multiples entiers d'une fréquence
de base f0 = 1/T, ou; T est la période de
x(t). Ce développement se présente ainsi :
 L'expression du membre
de droite est appelée série de Fourier. Effectuer une transformée de
Fourier consiste à trouver toutes les valeurs ak et
bk qui composent la série, connaissant la fréquence de base et
la fonction x(t). La transformée de Fourier est également
représentable par la fonction suivante
L'expression du membre
de droite est appelée série de Fourier. Effectuer une transformée de
Fourier consiste à trouver toutes les valeurs ak et
bk qui composent la série, connaissant la fréquence de base et
la fonction x(t). La transformée de Fourier est également
représentable par la fonction suivante
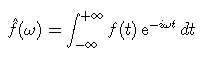 et
la transformée inverse par
et
la transformée inverse par
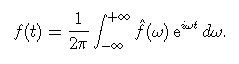
Le terme exponentiel est en fait décomposable en
Cos(2.pi.f0.t)+j.Sin(2.pi.f0.t).
Cette expression "complexe" comprend:
 une partie réelle
Cos(2.pi.f0.t) de fréquence f0 et une partie imaginaire
j.Sin(2.pi.f0.t) de fréquence f0
une partie réelle
Cos(2.pi.f0.t) de fréquence f0 et une partie imaginaire
j.Sin(2.pi.f0.t) de fréquence f0
Le résultat de l'intégration de cette expression est
 soit élevé:dans ce
cas le signal a un terme dominant à la fréquence f0
soit élevé:dans ce
cas le signal a un terme dominant à la fréquence f0
 soit faible:dans ce
cas le signal n'a pas de terme dominant à la fréquence f0
soit faible:dans ce
cas le signal n'a pas de terme dominant à la fréquence f0
 soit nul :dans ce cas
le signal ne contient pas de fréquence f0
soit nul :dans ce cas
le signal ne contient pas de fréquence f0
Comme l'intégration se fait de -infini(t)à+infini(t).Que le terme à la
fréquence f0 apparaisse à t1 ou t2 n' a pas d'importance sur l'intégration.C'est
pourquoi la transformée de Fourier n'est pas adaptée lorsque le signal est non
stationnaire(cad que sa fréquence varie avec le temps).
2a)Analyse de Fourier
Le désavantage de la décomposition en série de
Fourier est que la fonction bien que localisée en fréquence se retrouve très mal
localisée spatialement . Les informations portent sur les fréquences et non sur
la valeur de l'information à un instant. Pour celà a été imaginée l'ondelette
qui consiste à effectuer une sorte de décomposition de Fourier mais sur un
morceau de l'information. Ce morceau ayant une taille constante, on l'appelle
fenêtre. L'analyse de Fourier à fenêtre décompose donc le signal en faisant
parcourir le fenêtre sur tout le signal. Le désavantage de cette méthode
d'analyse du signal est que la fenêtre ayant une taille constante, celle-ci est
aveugle aux hautes et au basses fréquences.
2b)Les Fourier à fenêtre
Une fenêtre est une fonction régulière, qui
varie lentement et est bien localisée, cad qu'elle est nulle en dehors d'une
certaine zone, qu'on appelle son support.
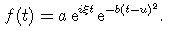 L'ensemble de ces
transformées de Fourier ainsi localisées forme la transformée de Gabor du
signal,elle fournit donc une analyse fréquentielle locale. Le signal peut être
synthétisé comme somme de gaborettes, qui ne sont autres que des sinusoïdes
localisées par des fenêtres du même type que celles qui sont utilisées pour la
transformation de Gabor. A chacune de ces gaborettes sont attachés une fréquence
et un temps bien déterminés. Le poids d'une gaborette dans un signal n'est autre
que la valeur de sa transformée de Gabor pour la fréquence et le temps
correspondants.
L'ensemble de ces
transformées de Fourier ainsi localisées forme la transformée de Gabor du
signal,elle fournit donc une analyse fréquentielle locale. Le signal peut être
synthétisé comme somme de gaborettes, qui ne sont autres que des sinusoïdes
localisées par des fenêtres du même type que celles qui sont utilisées pour la
transformation de Gabor. A chacune de ces gaborettes sont attachés une fréquence
et un temps bien déterminés. Le poids d'une gaborette dans un signal n'est autre
que la valeur de sa transformée de Gabor pour la fréquence et le temps
correspondants.
2c)Applications à la modélisation moléculaire
.Reconnaissance des formes
et surfaces des molécules
 HARMONIQUES SPHERIQUES
HARMONIQUES SPHERIQUES
Webmaster:
Last
revised:05/2001

 Une fréquence est l'inverse d'une
période.
Une fréquence est l'inverse d'une
période.
 Un signal monodimensionnel est
périodique de période T>0 s'il reste inchangé par une translation de T.
Un signal monodimensionnel est
périodique de période T>0 s'il reste inchangé par une translation de T.
 On appelle signal stationnaire un
signal dont le contenu fréquentiel ne change pas dans le temps.
On appelle signal stationnaire un
signal dont le contenu fréquentiel ne change pas dans le temps.
 Signal stationnaire
Signal stationnaire Signal non stationnaire
Signal non stationnaire
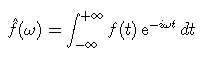
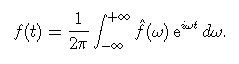
![]() une partie réelle
Cos(2.pi.f0.t) de fréquence f0 et une partie imaginaire
j.Sin(2.pi.f0.t) de fréquence f0
une partie réelle
Cos(2.pi.f0.t) de fréquence f0 et une partie imaginaire
j.Sin(2.pi.f0.t) de fréquence f0
![]() soit élevé:dans ce
cas le signal a un terme dominant à la fréquence f0
soit élevé:dans ce
cas le signal a un terme dominant à la fréquence f0
![]() soit faible:dans ce
cas le signal n'a pas de terme dominant à la fréquence f0
soit faible:dans ce
cas le signal n'a pas de terme dominant à la fréquence f0
![]() soit nul :dans ce cas
le signal ne contient pas de fréquence f0
soit nul :dans ce cas
le signal ne contient pas de fréquence f0