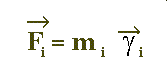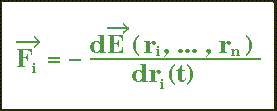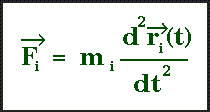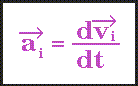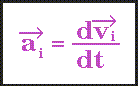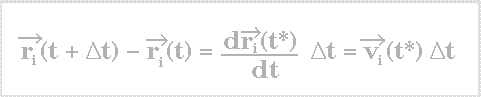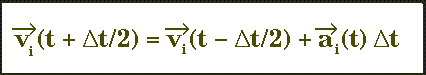CADCOM/MANUEL D'UTILISATION

DYNAMIQUE MOLECULAIRE
1)Definition
  La dynamique moléculaire consiste à étudier la trajectoire
  d'une molécule en appliquant les lois de la mécanique classique 
  newtonienne cad à simuler les mouvements atomiques au cours du temps.
  Ces mouvements correspondent à des vibrations autour
  d'un minimum ou au passage d'un minimum à un autre
  minimum d'énergie.
  Ainsi la dynamique moléculaire permet de s'extraire d'un minimum 
  local.
    

2)Principe de base
  Chaque atome de la molécule est considéré comme une 
  masse ponctuelle dont le mouvement est déterminé 
  par l'ensemble des forces exercées sur lui par
  les autres atomes en fonction du temps.
   . échelle de temps atomique:1 femtosec(10-15s)
  Les forces exercées sont considérées comme constantes.
  La molécule est donc perçue comme une entité dynamique
  dont les atomes modifient leurs positions spatiales
  au cours du temps.

3)Algorithme
  
  Au temps T,chaque atome i ,de coordonnées xi,yi,zi et
  de masse mi subira une accélération ai telle que


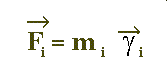         mi=masse de l'atome i
         ai=accélération de l atome i
         Fi=force agissant sur l'atome i

La dynamique moléculaire permet de calculer la force exercée sur 
chaque atome et fournit différentes informations sur la trajectoire 
(vitesse et position des atomes pendant un intervalle de temps 
spécifique, de l'ordre de 1 à 100 ps ).
La force F(i) qui s'exerce sur un atome i de coordonnées r(i) au temps t
est déterminée par dérivation de la fonction énergie potentielle . 


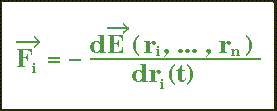         E :fonction de l'énergie potentielle totale d'interaction
         ri:coordonnées cartésiennes de l'atome i




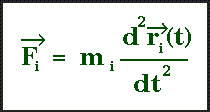 On peut alors intégrer les équations de mouvement et
 obtenir une trajectoire de chaque atome en fonction
 du temps.Pour celà,on utilise l'algorithme de Verlet.
 Elle consiste à calculer: 
  . les accélérations atomiques à partir des forces s'exerçant sur chaque 
  atome et des masses atomiques. 
  .les vitesses de chaque atome à partir des accélérations atomiques. 
   
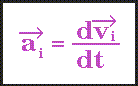  .les positions des atomes à partir des vitesses atomiques: 
  
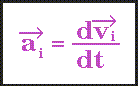  L'intégration de ces équations se fait en subdivisant la trajectoire en une 
série d'états discrets séparés par des intervalles de temps très courts dont la 
longueur définit le pas d'intégration delta t. Le déplacement d'un atome 
pendant l'intervalle de temps delta t est ainsi donné par l'équation: 

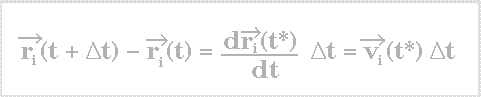Il est alors possible de déterminer l'accélération à partir de la seconde 
loi de Newton et la vitesse propre à chaque atome: 


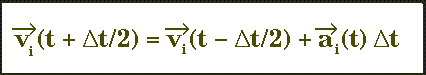La détermination de la vitesse permet d'obtenir la position de l'atome à 
l'aide de l'équation de précédemment énoncée à l'instant (t + delta t). 
La répétition de cette procédure à des intervalles de temps discrets en fonction 
de la vitesse aboutit à l'identification de la trajectoire.

 L'énergie totale du systéme doit être conservé durant
 toute la simulation.
L'intervalle de temps doit être choisi petit par rapport
à la période du mouvement de plus haute fréquence(
cad celui de l'hydrogéne.1 femtosec) pour éviter des
mouvements trop grands ce qui restreint la simulation à
quelques centaines de picosecondes à cause du temps
prohibitif du temps de calcul.

Température
 La température d'une molécule ou agitation thermique
 correspond à l'énergie cinétique des atomes de
 la molécule.


L'accélération est corrigée en intégrant la loi de
Stockes pour prendre en compte la viscosité éventuelle
(d'autres programmes utilisent plutôt la notion de frottement) 
La vitesse est ensuite calculée à partir de l'accélération
moyenne,puis ajustée pour maintenir une température constante.
On définit la température du bain (btemp),avec un
gradient de chauffe(tau) et un temps de relaxation 
timestep.

(SOMMAIRE)

Webmaster:
Last revised:05/2000